Advanced Image synthesis - Ward BRDF
TD2 - BRDF de Ward
1. Éclairage direct
Afin d’implementer la brdf on utilise la formule suivante :
$$ f_r(\vec{i}, \vec{o}) = \frac{\rho_s}{4 \times \pi \times \alpha_x \times \alpha_y \times \sqrt{(\vec{i} \cdot \vec{n}) \times (\vec{o} \cdot \vec{n})}} \times e^{-\frac{\left(\frac{\vec{h} \cdot \vec{x}}{\alpha_x}\right)^2 + \left(\frac{\vec{h} \cdot \vec{y}}{\alpha_y}\right)^2}{\left(\vec{h} \cdot \vec{n}\right)^2}} $$
Où : \(h = \frac{\vec{i} + \vec{o}}{\left\lVert \vec{i} + \vec{o} \right\rVert}\)
Afin de vérifier et visualiser la \(BRDF\) on utilise l’integrateur direct. Ainsi, on obtien les résultats suivants :
 $$\alpha_x = \alpha_y = 0.01$$ |
 $$\alpha_x = \alpha_y = 0.1$$ |
 $$\alpha_x = \alpha_y = 0.25$$ |
 $$\alpha_x = \alpha_y = 0.5$$ |
 $$\alpha_x = 0.2 ~~~ \alpha_y = 0.1$$ |
 $$\alpha_x = 0.5 ~~~ \alpha_y = 0.1$$ |
 $$\alpha_x = 0.1 ~~~ \alpha_y = 0.2$$ |
 $$\alpha_x = 0.1 ~~~ \alpha_y = 0.5$$ |
2. Échantillonnage uniforme de la BRDF
Dans cette partie on cherche à simuler un matériaux glossy. Pour ce faire on lance des rayons depuis la caméra. Quand ces rayons intercepte une surface, on echantillone \(N\) directions sur l’hemisphere orienté dans le plan tangeant à la surface. Puis pour chaque direction on lance un rayon pour évaluer leurs contribution qui sera pondérée par la \(BRDF\), le cosinus term et l’inverse de sa fonction de densité de probabilité (pdf). Ceci nous done l’estimateur suivant :
$$ \langle L_o \rangle = \frac{1}{N} \sum_{1}^{N} L_i \mathbf{p} \cdot \mathbf{n} \frac{1}{pdf} = \frac{\pi}{N} \sum_{1}^{N} L_i $$
Enfin on obtien les résultats suivants :
 $$\alpha_x = \alpha_y = 0.01$$ |
 $$\alpha_x = \alpha_y = 0.1$$ |
 $$\alpha_x = 0.5 ~~~ \alpha_y = 0.1$$ |
 $$\alpha_x = 0.1 ~~~ \alpha_y = 0.5$$ |
3. Échantillonnage préférentiel
Afin de réduire le vruit des images précedentes on vas chercher a echantilloner nos directions non plus dans tout l’hemisphere mais seulement dans le lobe de la \(BRDF\). Ceci est réalisable grace aux formules suivantes :
$$ \theta_h = \arctan\left(\sqrt{\frac{-log(\xi_u)}{\frac{\cos^2(\phi_h)}{\alpha_x^2}+\frac{\sin^2(\phi_h)}{\alpha_y^2}}}\right) $$
$$ \phi_h = \arctan\left(\frac{\alpha_y}{\alpha_x} \times \tan\left(2 \times \pi \times \xi_v \right)\right) $$
Ce qui nous permet de determiner les vecteurs \(\vec{h}\) et \(\vec{o}\) tel que:
$$ \vec{h} = \left[\sin\theta_h \times \cos\phi_h , \quad \sin\theta_h \times \sin\phi_h , \quad \cos\theta_h\right] $$
$$ \vec{o} = 2 \times \left(\vec{i}\cdot\vec{h}\right) \times \vec{h}-\vec{i}$$
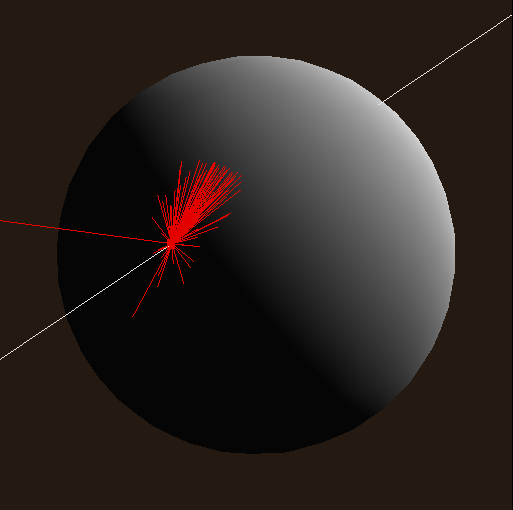
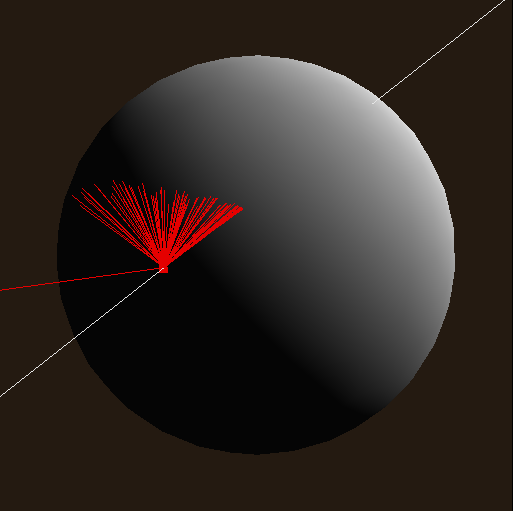
Ainsi, on peut visualiser les directions echantillonés avec cette méthode et les images résultantes :
 |
 |
 |
 |
 |
 |
 |
 |
| $$\alpha_x = \alpha_y = 0.01$$ | $$\alpha_x = \alpha_y = 0.1$$ | $$\alpha_x = 0.5 ~~~ \alpha_y = 0.1$$ | $$\alpha_x = 0.1 ~~~ \alpha_y = 0.5$$ |
En cherchant en integrer la partie diffuse d’un composant de Ward, on cherche à tirré maintenant soit une direction diffuse ou spéculaire. Pour ce faire on viens choisir entre l’un ou l’autre à l’aide du ratio suivant :
$$ \frac{\overline{specularColor}}{(\overline{specularColor} + \overline{diffuseColor})} $$
Avec ceci on obtiens les résultats suivants:
 $$\alpha_x = \alpha_y = 0.01$$ |
 $$\alpha_x = \alpha_y = 0.1$$ |
 $$\alpha_x = 0.5 ~~~ \alpha_y = 0.1$$ |
 $$\alpha_x = 0.1 ~~~ \alpha_y = 0.5$$ |