Advanced Image synthesis

Integration de Monte-Carlo 1D

J’utilise le code suivant afin d’evaluer l’integration de la fonction $f(x) = 5 x ^4$ :

double int_mc(double(*f)(double), double& varest, double a, double b, int n)
{
  double factor = 1. / n;
  double varest_factor = 1. / (n - 1);
  
  double result = 0.;
  double fx2 = 0.;
  varest = 0.;
  
  for (int i = 0; i < n; ++i) {
    double x = getX(a, b);

    double step_value = factor * f(x);
    fx2 += f(x) * f(x);  
    
    result += step_value;
  }

  varest = ((fx2 * factor) - (result * result)) * varest_factor;
  return result;
}

La fonction getX(double a, double b) retourne un double aléatoire compris entre a et b tel que :

double getX(double a, double b) {
  return (rand() / double(RAND_MAX)) * (b - a) + a;
}

Ceci nous permet donc d’obtenir l’estimation de l’integrale de la fonction $f(x)$ et sa variance estimée. Enfin pour obtenir sa variance analytique il nous faut integrer la formule suivante :

$$ \begin{align} \sigma ^2 & = \frac{1}{N} \int _0 ^1 (5 x^4 -1)^2 \, dx \\ & = \frac{1}{N} \int _0 ^1 (25 x^8 - 10 x^4 + 1) \, dx \\ & = \frac{1}{N} \left[\frac{25}{9} x^9 - \frac{10}{5} x ^5 + x \right]_0 ^1 \\ & = \frac{1}{N} (\frac{25}{9} - 2 + 1) \\ & = \frac{1}{N} * \frac{16}{9} \end{align} $$

Ainsi on peut estimer pour un nombre gradissant d’échantillons les valeurs suivantes : l’erreur d’estimation, la variance numérique, la variance analytique. On obtient donc :

plot

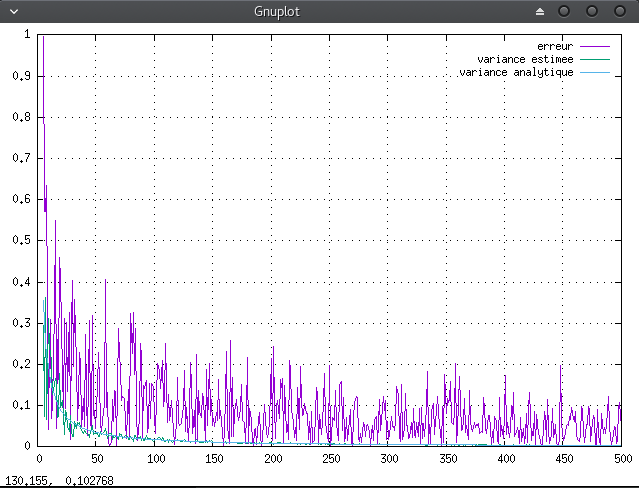
Anti-Aliasing

L’anti-aliasing a bien été implémenter en utilisant une grille réguliere et une jitterid grid pour integrer les différents rayons nécessaires. On peut voir dessous les resultats pour la scene tw.scn avec a gauche sans anti-aliasing, au centre celui utilisant la grille régulière et a droite celui stratifié (on ne parle pas de parquet ici).

On peut aussi voir la difference entre les deux méthodes d’anti-aliasing avec des valeurs de samples differentes ci-dessous :

Sources étendues

Echantillonage de Monte-Carlo

En echantillonnant les sources de lumière de type AreaLight On obtients les résultats suivants.

Source Texturée

Afin d’obtenir l’aplication d’une texture à l’éclairage d’une AreaLight il a fallut moddifier la methode AreaLight::intensity tel que :

Color3f AreaLight::intensity(const Point3f &x, const Point3f &y) const {
    Vector3f dir = (x-y);
    float d2 = dir.squaredNorm();
    Color3f intensity = m_intensity / d2;
    if(m_texture) {
        // TODO
        float i = (y - position()).dot(uVec()) / size().x();
        float j = (y - position()).dot(vVec()) / size().y();

        Color3f texture_value = (*m_texture)(j * m_texture->cols(), i * m_texture->rows());
        intensity *= texture_value;
    }
    return std::max(0.f,dir.normalized().dot(direction())) * intensity;
}

Et grace a cela on peut donc venir lire dans la texture et appliquer une couleur spécifique a l’éclairage. On obtient avec ceci les résultats suivants.

Ambiante Occlusion

Échantillonnage d’un hémisphère

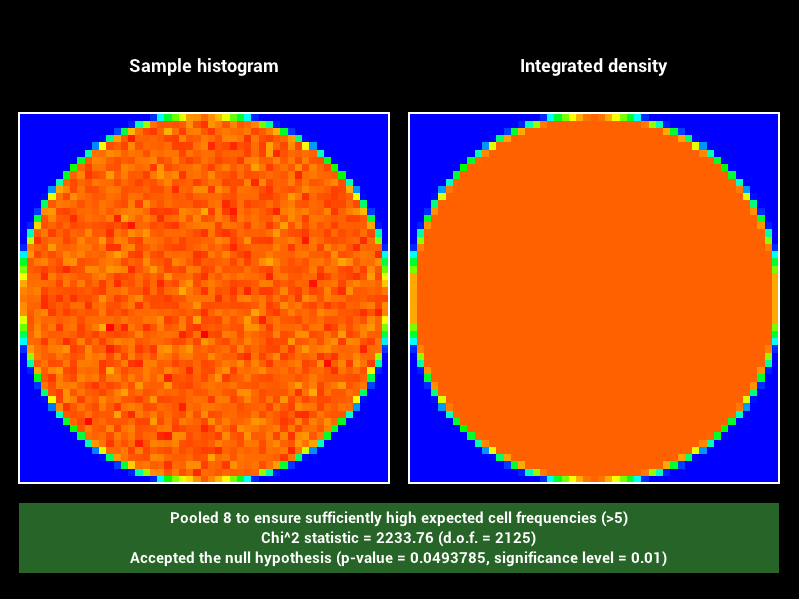
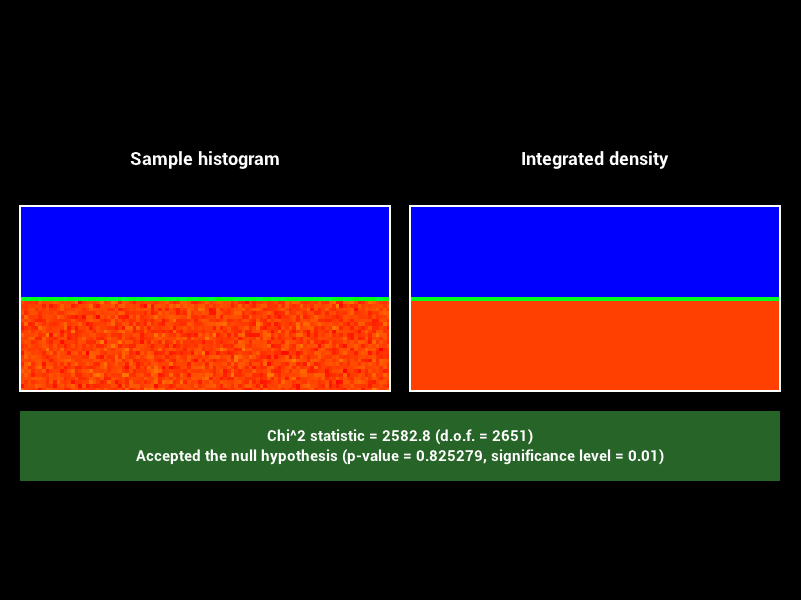
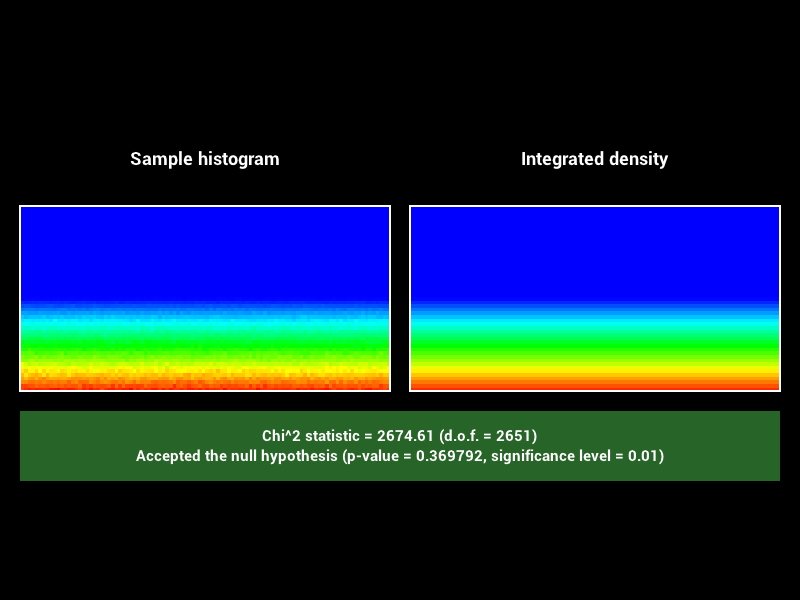
Après implémentation des differentes méthodes on obtiens les résultats suivants. Dans l’ordre, de gauche a droite, squaretoDisk, squaretoUniformHemisphere, squaretoCosineHemisphere.

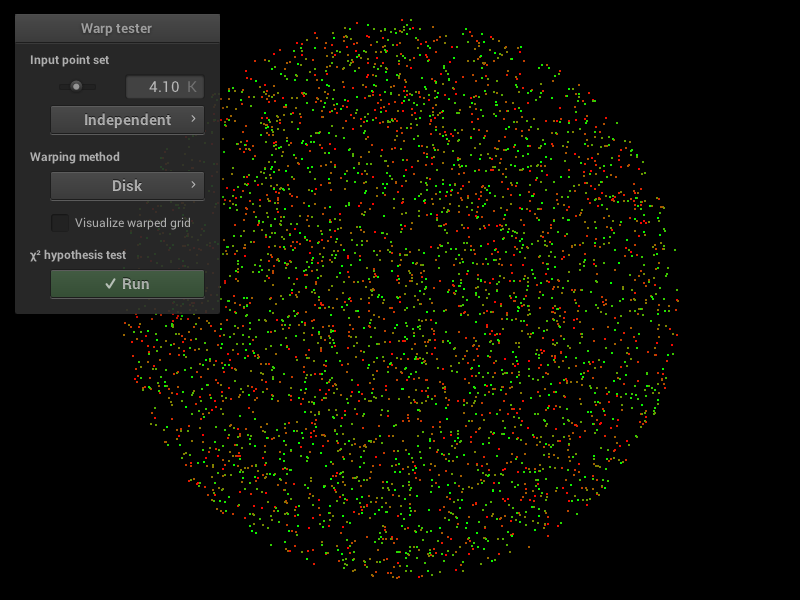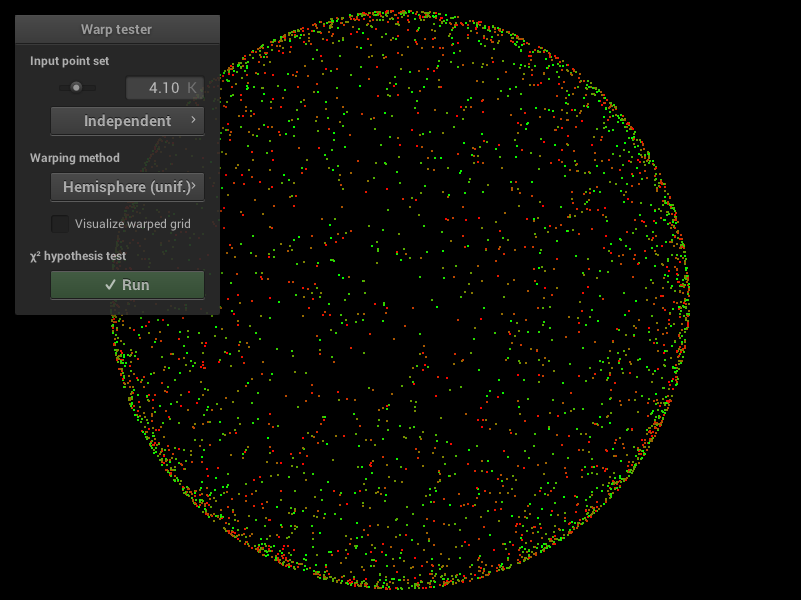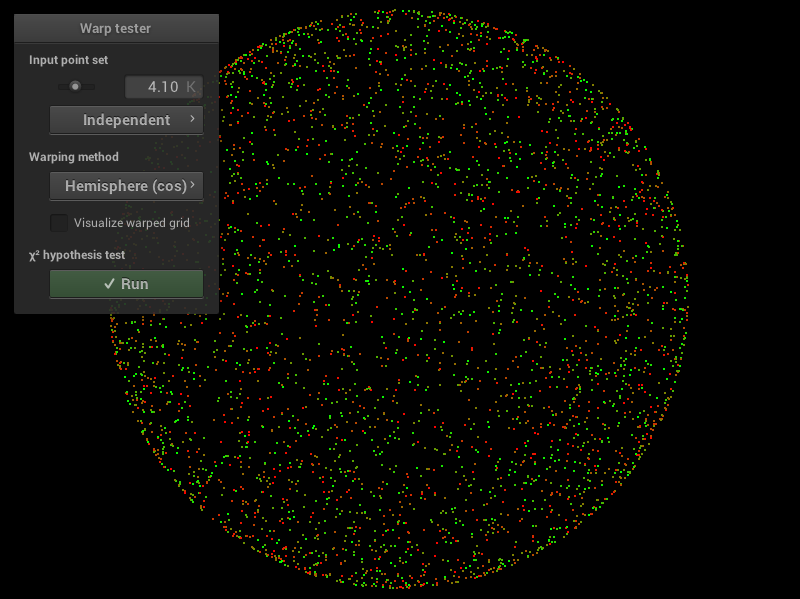Calcul de l’AO

Pour calculer l’ambiant occlusion on effectue les opérations suivantes. On lance des rayons depuis la caméra, quand on touche une surface, on vient échantillonner un certains nombre de points dans un hémisphère orienté selon le repère local au point d’intersection du premier rayon. Pour chacun de ces échantillons on vas lancer un rayon pour calculer la visibilité du point d’intersection selon une direction définie par l’échantillon. Ainsi, en sommant l’ensemble de ces indication de visibilités puis en les moyennant on integre la visibilité du point d’intersection sur la surface. Avec cette méthode on obtiens les résultats suivants.

Liens utiles

Sujet du TD

Code source

Posts