Advanced Image synthesis - Monte-Carlo
Séance 1 du 06/09/2017
Integration de Monte-Carlo
On va calculer des intégrales :
Estimation de Pi : Aire du disque unitaire ?
On vient prendre un carré contenant un quart du disque et on viens distribuer des echantillons dans le carré. En faisant le rapport entre les echantillons dans le quart de disque par rapport a ceux dans le carré on obtiens Pi.
Precision correcte de Pi a 4 decimales : 100 000 000 000 d’échantillons.
Integration en 1D :
$$ I = \int _a ^b f(x) dx $$
Méthodes de Simpson : Faire la somme des rectangle en utilisant des pas sur la dimmension. On peut utiliser des trapèzes

Estimateur de monte-carlo :
$$ \langle I ^N \rangle = (b - a)\frac{1}{N} \sum _{i = 0} ^{N - 1} f(X_i) $$
avec \(X_i = a + \epsilon(b - a)\)
On viens prendre N échantillons aléatoire, on evalue leurs valeurs et on calcule l’aire, on vient faire la moyenne de ces aires.
Variable aléatoire discrete :
Probabilité pi associé à chaque événement xi
Esperance : Sommes de tout les evenements possibles de la probabilité fois l’evenement.
$$ E[x] = \sum _i p _i x _i $$
Variance : carré de l’ecart type. L’esperance de la distance a l’esperance au carré.
$$ \sigma ^2 = E[(x - E[x]) ^2] = \sum _i (x _i - E[x])^2 p _i $$
$$ \sigma ^2 = E[x ^2] - (E[x])^2 = \sum _i x _i ^2 p _i - (\sum _i x _i p_i)^2 $$
Proprietes :
- Esperance :
$$ E(x + y) = E[x] + E[y] $$
$$ E(ax) = a E[x] $$
- Variance :
$$ \sigma ^2 [x + y] = \sigma ^2 [x] + \sigma ^2 [y] + 2 Cov[x,y] $$
Avec \(Cov(x,y) = E[xy] - E[x]E[y]\)
$$ \sigma ^2[ax] = a ^2 \sigma ^2 [x] $$
Fonction de v.a. discretes :
Soit f(x) la fonxtion ou x prends la valeur xi avec proba pi => aussi une variable aléatoire
Espérance :
$$ E[f(x)] = \sum _{i = 1} p _i f(x _i) $$
Variance :
$$ \sigma ^2 = E[(f(x) - E[f(x)]) ^2] $$
Variables aléatoire à densité
PDF : Densiré de probabilité - \(p(x)\) :
$$ Pr(a \le x \le b) = \int _a ^b p(x)dx $$
p(x) probabilité que x soit dans l’intervalle plus un delta x.
CDF : Fonction de répartition - P(y) :
$$ P(y) = Pr(x \le y) = \int _{- \infty} ^y p(x)dx $$
Probabilité que x soit inferieur a y.
Variables aléatoire continue :
PDF en haut et CDF en bas pour une loi normale :
Loi normale :
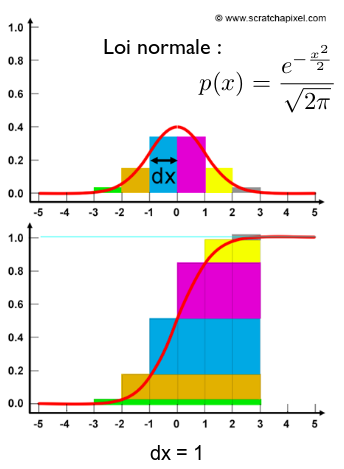
Proprietés : (formula)
- \(\forall x, p(x) \ge 0\)
- \(\int _{- \infty} ^\infty p(x)dx = 1\)
- \(p(x) = \frac{dP(x)}{dx}\)
$$ Pr(a \le x \le b) = P(b) - P(a) = \int _a ^b p(x)dx $$
Variables aléatoires à densité
Esperance :
$$ E[x] = \int _{- \infty} ^\infty x p(x) dx $$
$$ E[f(x)] = \int _{- \infty} ^\infty f(x) p(x) dx $$
Variance : (formula)
Somme pondérée de v. a.
Soient N variables aléatoire, avec xi des variables indépendantes identiquement distribuées suivant la mmêe loi p(x) et :
$$ G = \sum _{j = 1} ^N w _j g(x _j) = \sum _{j = 1} ^N w _j g _j (x) $$
Espérance :
$$ E[G] = \sum _{j = 1} ^N w _j E[g _j (x)] $$
Si \(w _j = \frac{1}{N} \forall j\) , \(G = \frac{1}{N} \sum _{j = 1} ^N g _j (x)\)
$$ E[G] = \dots = E[g(x)] $$
Car comme ils suivent tous la même loi de probabilité et qu’ils ont la même distribution, alors leurs espereance sera la même.
G devient donc un estimateur de l’espérance de g(x)
Variance :
$$ \sigma ^2[G(x)] = \dots = \frac{\sigma ^2[g(x)]}{N} $$
Plus N est grand, meilleur G devient un estimateur de l’esperance. Sa deviation standard sigma diminu en racine de N.
Estimateur de Monte-Carlo
Estimation de \(I = \int _a ^b f(x)dx\) à l’aide de N échantillons tirés aléatoirements dans \([a,b]\) selon la densité \(p(x)\)
$$ \langle I ^N \rangle = \frac{}{} \sum _{i = 0} ^{N -1} \frac{f(x _i)}{p(x _i)} $$
Esperance :
$$ E[\langle I ^N \rangle] = \dots = I $$
Variance :
$$ \sigma ^2 [\langle I ^N \rangle] = \frac{1}{N} \int (\frac{f(x)}{p(x)} - I) ^2 p(x)dx $$
==> Convergence de l’estimateur de racine de N ==> 4 fois plus d’échantillons pour diminué l’erreur par 2
Estimateur de la variance : Avec les me N échantillons, on peut estimer la variance de <I^N> avec l’estimateur :
$$ \langle \sigma ^2 [ \langle I ^N \rangle ] \rangle = \frac{\frac{1}{N} \sum _{i = 1} ^N (\frac{f(x _i)}{p(x _i)})^2 - (\frac{1}{N} \sum _{i = 1} ^N \frac{f(x _i)}{p(x _i)})^2}{N - 1} $$
On utilise les mêmes echantillons pour estimer la variance de l’estimateur.
Bilan
Etapes :
- Générer N echantillons delon la PDF
- Evaluer la fonction à interer en ces échantillons
- Moyenner ces évaluation en divisant par la PDF
Pros :
- Pas de contraintes sur la fonction
- Même convergence quelle que soit la dimenssion
- Implementation simple
Cons :
- Convergence lente
- Implementation efficace pas toujours facile
Séance 2 du 13/09/2017
Comment generer les echantillons selon une PDF
Méthode de la transformée inverse
Cas discret :
On veut choisir \(x _i\) avec une probabilité \(p _i\)
La CDF discrete associé a pi vaut : \(P _i = \sum _{j = 1} ^i p _j\)
Tirer un nomre aléatoire \(\xi\) uniformement sur [0, 1[
Trouver k tel que :
ADD THINGS
==> Probabilité que \(\xi\)
Calcul de la CDF discrete en O(N) Recherche de k en O(log2(N))
Cas continue : idem ! \(y = P ^{-1} (\xi)\)
==> Necessité d’inverser la CDF … pas toujours possible)
En plus haiutes dimension ?
Si densité séparable : \(p(x, y) = p _x (x) p _y (y)\) .On a donc un échantillonage indépendant ID de \(p _x\) et \(p _y\)
Sinon, calcul de la densité marginale :
$$ p(x) = \int p(x,y)dy $$
Et de la densité conditionelle :
| $$ p(y | x) = \frac{p(x,y)}{p(x)} $$ |
| Et echantillonage independant ID de \(p(x)\) et $$ p(x | y) $$ |
Méthode de rejet
Si la valeur maximale de \(p(x)\) dans \([a,b]\) est M, alors considerer la fonction 2D dans \([a,b] x [O,M]\)
L’echantilloner uniformement en \((x,y)\) et rejetter les échantillons si \(p(x) < y\).
Pros :
- Valide pour toute PDF
- en toute dimension
Cons :
- potentiellement ineficace
Comment accelerer la convergence
Reductionb de la variance
Choisir la PDF pour controller la vitesse de convergence.
Echantillonage préférentiel
Idée : echantilloner selon ine PDF p(x) non-uniforme pour minimiser la variance de l’estimateur.
On peut montrer que l’optimum vaut :
| $$ p(x) = \frac{ | f(x) | }{\int f(x)dx} $$ |
Probleme : on ne sait pas intégrer \(f\) …
Stratégies d’echantillonage
- Stratification
- Quasi-Monte-Carlo
Stratification
Proprietes désirées
- Distribution uniforme sur la surace
- distribution uniforme apres projection sur les axes
- ==> Maximiser la plus petite distance entre 2 échantillons pour eviter les zones …
Régulier
Distribuer sur une grille réguliere
- échantillons corrélés
- aliasing : la régularité se voit dans l’image
Aléatoire uniforme
Trier uniformement dans \([0,1[ x [0,1[\)
- remplace l’aliasing par du bruit
- nécessite moins d’echantillons
- localement pas uniforme
Stratified sampling
- Subdiviser le domaine en sous-regions sans recouvrement
- Trier un échantillon par stratum
- reduit les agrégats, mais pas toujours uniforme
Latin Hypercube Sampling (LHS)
- Generer un echantillon par cellule de la diagonale
- Brassage aléatoire des echantillons dans chaque dimension
- distribution reste uniforme selon les axes
- permet de generer un nombre arbitraire d’echantillons
Mais pas de garantie quant a l’uniformité globale des echantillons 2D.
en plus haute dimensions
Generer \(n ^d\) echantillons
- d = 2 : Surface
- d = 3 : surface + temps
- d = 5 : pixel + temps + lentille
Au lieu de generer \(n ^5\) echantillons, generer \(n^2 + n + n ^2\) echantillons et les combiner aléatoirement.
Poisson disk sampling
Distribution des photorécepteurs de la rétine
Distribution aléatoire, mais distance minimum entre 2 échantillons
Dart Throwing
- générer un echantillon aléatoirement et tester s’il est valide
- convergence non garantie
Best-candidates
- Approximation :
- génerer aléatoirement k candidats
- garder celui étant le plus éloigné de tous les précédents